This task is intended to engage students in considering how margin of error can be estimated from examining the results of repeated simple random sampling.

Finding lost objects is not always an easy task, even when you have knowledge of a general location. Consider the following scenario: you have lost a small object, such as a class ring, in a small park see map 1. It is getting dark and you have your pen light flashlight available. If your light shines on the ring, you assume that you see it. You cannot possibly search 100% of the region. Determine how you will search the park in minimum time. An average person walks approximately 4 mph. You have about 2 hours to search. Determine the chance you will find the lost object.https://mathmodels.org/Problems/2011/HIMCM-B/index.html

This lesson unit is intended to help you assess how well students are able to solve problems involving area and arc length of a sector of a circle using radians. It assumes familiarity with radians and should not be treated as an introduction to the topic.

The purpose of this Illustrative Mathematics task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context.

This task involves several different types of geometric knowledge and problem-solving: finding areas of sectors of circles, using trigonometric ratios to solve right triangles, and decomposing a complicated figure involving multiple circular arcs into parts whose areas can be found.

This task is intended for instructional purposes only. It provides an opportunity to model a concrete situation with mathematics.

As online stores start to compete with traditional brick and mortar stores the goal is to combine the benefits of both types of businesses. Brick and mortar stores provide the benefit of seeing the actual items, picking up your purchase right away, and not having to pay for shipping. But, sometimes the store is not convenient to your location, or you do not have time to go shopping. Online stores offer the convenience of shopping from home and the added benefit, in many cases, of no additional sales or other taxes. And, with international shipping, many more items are available to shoppers all over the globe via the Internet. For the purposes of this HiMCM problem, we will use an example from the United States.

This is a foundational geometry task designed to provide a route for students to develop some fundamental geometric properties that may seem rather obvious at first glance. In this case, the fundamental property in question is that the shortest path from a point to a line meets the line at a right angle, which is crucial for many further developments in the subject.

The purpose of this task is to have students complete normal distribution calculations and to use properties of normal distributions to draw conclusions. The task is designed to encourage students to communicate their findings in a narrative/report form in context not just simply as a computed number.

This task provides a geometric context for working with ratios and algebraic equations. Students will create and then solve an algebraic equation describing a remarkable shape, the silver rectangle.

The goal of this task is to study if the analogue of the AA criterion for similarity of triangles holds for different types of quadrilaterals.

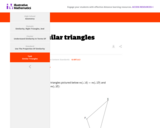
This task works toward establishing the AA criterion for similarity of triangles by providing a detailed sequence of transformations that moves one of the given triangles to the other.

The goal of this task is to work on showing that all circles are similar using these two different methods, the first visual and the second algebraic.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The goal of this task is to provide a geometric explanation for the relationship between the sine and cosine of acute angles.

Winter is coming! In February 2018, PyeongChang, South Korea will host the Winter Olympics. And, in 2022, Beijing, China will be the host city. The Winter Olympics have over fifty ski related events in the disciplines of Alpine, Nordic, Cross-Country, Ski Jumping, Snowboarding, and Freestyle.

Skyscrapers vary in height , size (square footage), occupancy rates, and usage. They adorn the skyline of our major cities. But as we have seen several times in history, the height of the building might preclude escape during a catastrophe either human or natural (earthquake, tornado, hurricane, etc). Let's consider the following scenario. A building (a skyscraper) needs to be evacuated. Power has been lost so the elevator banks are inoperative except for use by firefighters and rescue personnel with special keys.

Build a mathematical model to clear the building within X minutes. Use this mathematical model to state the height of the building, maximum occupation, and type of evacuation methods used. Solve your model for X = 15 minutes, 30 minutes, and 60 minutes.