The purpose of this task is to apply the definition of a parallelogram in the context of a geometric construction.

This simple conceptual task focuses on what it means for a number to be a solution to an equation, rather than on the process of solving equations.

This task can be implemented in a variety of ways. For a class with previous exposure to properties of perpendicular bisectors, part (a) could be a quick exercise in geometric constructions, and an application of the result. Alternatively, this could be part of an introduction to perpendicular bisectors, culminating in a full proof that the three perpendicular bisectors are concurrent at the circumcenter of the triangle.

This is a simple exercise in creating equations from a situation with many variables. By giving three different scenarios, the problem requires students to keep going back to the definitions of the variables, thus emphasizing the importance of defining variables when you write an equation.

This task gives the important characterization of the perpendicular bisector of a line segment as the set of points equidistant from the endpoints of the segment.

A group of four friends want to go to Polygon Paradise Park next summer. Polygon Paradise Park is a small amusement park open from 9am to 9pm. The park has ten rides of different types and thrill levels. The Trapezoid Show, a location with several different performances throughout the day, offers a circus acrobatics show, a magic show, and evening fireworks. The Games building has both arcade and carnival games. Food options include the Triangle Restaurant, the hot dog stand, and the ice cream cart. The hot dog stand and the ice cream cart are “take away” options, while the Triangle Restaurant requires 30-60 minutes to sit at a table and enjoy a meal. The restrooms (WC) are centrally located in the park for easy access. Visitors can purchase souvenirs in the gift shop located near the park entrance.

This task might be used as either practice with polynomial arithmetic or as an introduction to the binomial theorem, providing a process for raising binomials to powers without dredging through many repetitive applications of the distributive law.

The goal of this Illustrative Mathematics task is to practice making calculations with complex numbers and to visualize what happens when two complex numbers are multiplied.

The next Olympic Games are being hosted by Paris, France and will be held 26 July - 11 August 2024. The International Olympic Committee (IOC) wants to prepare by ordering enough medals and flags for the medal ceremonies. The IOC wants to make sure they have enough medals and flags for all the ceremonies to avoid being embarrassed. The IOC also does not want to waste money, however, by ordering too many medals and flags that will not be used. Therefore, the IOC has asked your team at MidMCM Olympic Consultants to provide models they can use to determine how many medals and flags they will need.

Have you ever been traveling down a highway when you see one or both of these signs?

In some cases, the road simply loses a lane as it enters a less traveled section. In other cases, the road narrows because of construction or roadwork. When this happens on a fairly busy highway, it may be a recipe for road rage*.

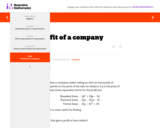
This task compares the usefulness of different forms of a quadratic expression. Students have to choose which form most easily provides information about the maximum value, the zeros and the vertical intercept of a quadratic expression in the context of a real world situation. Rather than just manipulating one form into the other, students can make sense out of the structure of the expressions.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The goal of this task is to use the unit circle and rigid transformations in order to establish some fundamental trigonometric function identities.

The purpose of this task is to prove the Pythagorean theorem using similar triangles.

This task has two separate goals: the first is to solve a pair of equations, one quadratic and the other linear. The second goal is to observe that a point, such as (35,45), that lies on C gives rise to a Pythagorean triple, in this case the triple (3,4,5).

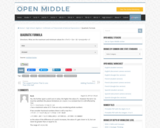
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

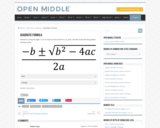
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

This task belongs to a series of three tasks that presents students with a sequence of tile figures with the property that the n-th figure in the sequence has f(n) tiles, for some quadratic function f.

This task belongs to a series of three tasks that has students process a sequence of tile figures with the property that the n-th figure in the sequence has f(n) tiles, for some quadratic function f.

The purpose of the task is to show students a situation where squaring both sides of an equation can result in an equation with more solutions than the original one.