The purpose of this task is to help provide geometric intuition for the algebraic process called ''completing the square.''

This task has the dual purpose of having students apply geometric volume formulas, and to have them reason about modeling with geometric figures.

The goal of this task is to establish formulas for volumes of right prisms and cylinders.

The goal of this task is to calculate the volume of a particular pyramid with square base, which is easily reasoned by viewing it as one sixth of a cube.

Fresh water is the limiting constraint for development in much of the United States. Devise an effective, feasible, and cost-efficient national water strategy for 2010 to meet the projected needs of the United States in 2025. In particular, address storage and movement, de-salinization, and conservation as some of the possible components of your strategy. Consider economic, physical, cultural, and environmental effects. Provide a position paper for the United States Congress outlining your approach, its costs, and why it is the best choice for the nation.

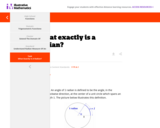
Radians are often mysterious to students, yet they are a very straight forward way to measure an angle by relating the measure of the angle to the length of the arc on the unit circle it subtends. This task is not designed to discover the definition of radian, rather it allows students to make meaning out of the definition.

In 1945, Noah Sentz died in a car accident and his estate was handled by the local courts. The state law stated that 1/3 of all assets and property go to the wife and 2/3 of all assets go to the children. There were four children. Over the next four years, three of the four children sold their shares of the assets back to the mother for a sum of $1300 each. The original total assets were mainly 75.43 acres of land. This week, the fourth child has sued the estate for his rightful inheritance from the original probate ruling. The judge has ruled in favor of the fourth son and has determined that he is rightfully due monetary compensation. The judge has picked your group as the jury to determine the amount of compensation.

Use the principles of mathematical modeling to build a model that enables you to determine the compensation. Additionally, prepare a short one-page summary letter to the court that explains your results. Assume the date is November 10, 2003.

1. Identify and analyze the major factors that you consider crucial to limiting the Earth’s carrying capacity for human life under current conditions.

2. Use mathematical modeling to determine the current carrying capacity of the Earth for human life under today’s conditions and technology.

3. What can mankind realistically do to raise the carrying capacity of the Earth for human life in perceived or anticipated future conditions? What would those conditions be?

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

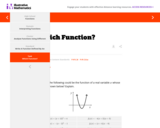
The task addresses knowledge related to interpreting forms of functions derived by factoring or completing the square. It requires students to pay special attention to the information provided by the way the equation is represented as well as the sign of the leading coefficient, which is not written out explicitly, and then to connect this information to the important features of the graph.

We read all the time in the sports pages about an athlete being called the G.O.A.T. - the Greatest Of All Time. What does that really mean and how can that truly be determined? For the purpose of this IM2C problem, we consider two types of “sports” – and, we allow “sports” to be defined broadly.

The goal of this task is to solve an equation involving a radical and then verify whether the solutions of the resulting quadratic equation are relevant.

This task is designed to help students understand statistics as a process for making inferences about population parameters based on a random sample from that population.

The purpose of this task is to assess (1) ability to distinguish between an observational study and an experiment and (2) understanding of the role of random assignment to experimental groups in an experiment.

The purpose of this task is to give students practice writing a constraint equation for a given context.

The purpose of this task is to have students derive the formula for the sum of a specific finite geometric series. In determining the total number of views the YouTube video has, students will first come across the sum of the terms of a geometric sequence. Without a formula, students will have to calculate this sum by adding each term individually. By the end of the task, the students will have come up with a formula that will help them find the sum much quicker than by rote calculation.

This task builds on ''Zeroes and factorization of a quadratic function'' parts I and II. The teacher may wish to recall the result from the first of these tasks, generalized to the polynomials of degree d considered here.

The level of the task is appropriate for assessment but since its intention is to provide extra depth to the standard A-APR.2 it is principally designed for instructional purposes only.

For a polynomial function p, a real number r is a root of p if and only if p(x) is evenly divisible by xr. This fact leads to one of the important properties of polynomial functions: a polynomial of degree d can have at most d roots. This is the first of a sequence of problems aiming at showing this fact.

This task is intended for instructional purposes to help students see more clearly the link between factorization of polynomials and zeroes of polynomial functions.