The goal of this task is to work on producing a quadratic equation from an arithmetic context.

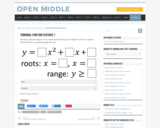
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Recent events have reminded us about the devastating effects of distant or underwater earthquakes. Build a model that compares the devastation of various-sized earthquakes and their resulting Tsunamis on the following cities: San Francisco, CA; Hilo, HI; New Orleans, LA; Charleston, SC; New York, NY; Boston, MA; and any city of your choice. Prepare an article for the local newspaper that explains what you discovered in your model about one of these cities.

Given the graph of a function students must find the value of 2 variables.

Given the graph of a function students must find the value of 2 variables.

This task focuses on the fact that exponential functions are characterized by equal successive quotients over equal intervals. This task can be used alongside F-LE Equal Factors over Equal Intervals.

This task provides a preliminary investigation of mathematical modeling using linear functions. In particular, students are asked to make predictions using a linear model without ever writing down an equation for a line. As such, the task could be used to motivate or introduce the observation that linear functions are precisely those that change by constant differences over equal intervals.

The purpose of this task is to deepen student understanding of the standard deviation as a measure of variability in a data distribution.

This lesson helps students understand these two types of data and choose the best type of graph or measure appropriate to each.

Trains arrive often at a central Station, the nexus for many commuter trains from suburbs of larger cities on a "commuter" line. Most trains are long (perhaps 10 or more cars long). The distance a passenger has to walk to exit the train area is quite long. Each train car has only two exits, one near each end so that the cars can carry as many people as possible. Each train car has a center aisle and there are two seats on one side and three seats on the other for each row of seats.

This task deals with a student error that may occur while students are completing F-IF Average Cost.

The purpose of the task is to explicitly identify a common error made by many students, when they make use of the "identity" f(x+h)=f(x)+f(h). The task has students find a single explicit example for which the identity is false, but it is worth emphasizing that in fact the identity fails for the vast majority of functions.

Successful work on this task involves modeling a bank account balance with an exponential function and then solving an exponential equation arising from the given information. This can be done either by extracting a root or taking a logarithm: either method will require a calculator in order to evaluate the expressions. Students will also need to be familiar with the context of annual interest and of compounding interest.

This interactive applet asks the student to connect points on a plane in order to build a function and then test it to see if it's valid.

This task is meant to be a straight-forward assessment task of graph reading and interpreting skills. This task helps reinforce the idea that when a variable represents time, t=0 is chosen as an arbitrary point in time and positive times are interpreted as times that happen after that.

Fresh water is the limiting constraint for development in much of the United States. Devise an effective, feasible, and cost-efficient national water strategy for 2010 to meet the projected needs of the United States in 2025. In particular, address storage and movement, de-salinization, and conservation as some of the possible components of your strategy. Consider economic, physical, cultural, and environmental effects. Provide a position paper for the United States Congress outlining your approach, its costs, and why it is the best choice for the nation.

The principal purpose of this Illustrative Mathematics task is to explore a real-world application problem with algebra, working with units and maintaining reasonable levels of accuracy throughout.

Given two points on a plane, students will demonstrate an understanding of unique linear function, unique exponential function, and quadratic function.