This problem shows that an exponential function takes larger values than a cubic polynomial function provided the input is sufficiently large.

This task is designed to help students learns how to Interpret functions that arise in applications in terms of the context.

A ladder 5 meters long is leaning against a vertical wall with its foot on a rug on the floor. Initially, the foot of the ladder is 3 meters from the wall. The rug is pulled out, and the foot of the ladder moves away from the wall at a constant rate of 1 meter per second. Build a mathematical model or models for the motion of the ladder. Use your model (or models) to find the velocity at which the top of the ladder hits the floor and the distance the top of the ladder will be from the wall at the moment that it hits the ground.

This Illustrative Mathematics task provides students the opportunity to make use of units to find the gas need to make some sensible approximations.

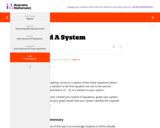
The purpose of this task is to encourage students to think critically about both the algebraic and graphical interpretation of systems of linear equations. They are expected to take what they know about solving systems of linear equations, and then reverse the usual process.

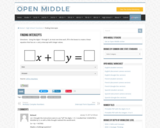
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The goal of this task is to present students with real world and mathematical situations which can be modeled with linear, exponential, or other familiar functions. In each case, the scenario is presented and students must decide which model is appropriate.

In this task students are asked to find all quadratic functions described by given equations.

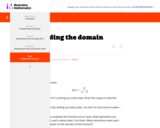
The purpose of this task is to introduce the idea of the domain of a function by linking it to the evaluation of an expression defining the function.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The purpose of this task is to use fixed points at a tool for studying and classifying rigid motions of the plane.

The purpose of this problem is to have students compose functions using tables of values only. Students are asked to consider the meaning of the composition of functions to solidify the concept that the domain of g contains the range of f.

Your team has been approached by the Forest Service to help allocate resources to fight wildfires. In particular, the Forest Service is concerned about wildfires in a wilderness area consisting of small trees and brush in a park shaped like a square with dimensions 80 km on a side. Several years ago, the Forest Service constructed a network of north-south and east-west firebreaks that form a rectangular grid across the interior of the entire wilderness area. The firebreaks were built at 5 km intervals.

Wildfires are most likely to occur during the dry season, which extends from July through September in this particular region. During this season, there is a prevailing westerly wind throughout the day. There are frequent lightning bursts that cause wildfires.

The problem requires students to not only convert miles to kilometers and gallons to liters but they also have to deal with the added complication of finding the reciprocal at some point. In the USA we use distance per unit volume to measure fuel efficiency but in Europe we use volume per unit distance. Furthermore, the unit of distance is not simply 1 km but rather 100 km.

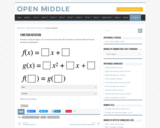
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Thousands of species of plants and animals face threats that could result in their extinction, while biodiversity conservation actions that could save them are often available. Conservation managers face difficult decisions when there is limited funding for biodiversity conservation. Managers need to decide which projects they should fund to best achieve their objectives, not the least of which is to save the most species. This is particularly important if the benefits of certain conservation actions vary across projects, the costs of these actions for specific projects differ, and the available funding for these actions is considerably less than is needed to support all proposed projects.

It appears from the economic reports that the world uses gasoline on a very short supply and demand scale. The impact of any storm, let alone Hurricane Katrina, affects the costs at the pumps too quickly. Let's restrict our study to the continental United States.

Thirteen straightedge and compass constructions are described and illustrated. The original version, in Word format, can be downloaded and distributed.

A small company wants to give raises to their 5 employees. They have $10,000 available to distribute. Imagine you are in charge of deciding how the raises should be determined.

The United States can address its national carbon footprint in two ways: by reducing carbon dioxide emissions or by increasing carbon dioxide consumption (sequestration). Assume that the total U.S. carbon dioxide emissions are capped at 2007-2008 levels indefinitely. What should the U.S. do to increase carbon dioxide consumption to achieve national carbon neutrality with minimal economic and cultural impact? Is it even possible to achieve neutrality? Model your solution to show feasibility, effectiveness, and costs. Prepare a short summary paper for the U.S. Congress to persuade them to adopt your plan.