This real-life modeling task could serve as a summative exercise in which many aspects of students' knowledge of functions are put to work.

This lesson contains an applet that allows students to explore translations, reflections, and rotations.

In air transportation, efficiency is time and time is money. Even small delays in the schedules of passenger airplanes result in lost time for both air carriers and their passengers. During any passenger flight, there are two time-consuming operations that depend mostly on human behavior: boarding and disembarking the aircraft.

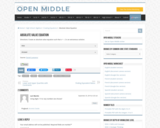
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

This task asks students to solve systems of linear equations exactly and approximately (e.g., with graphs), focusing on pairs of linear equations in two variables.

This task is a somewhat more complicated version of ''Accurately weighing pennies I'' as a third equation is needed in order to solve part (a) explicitly.

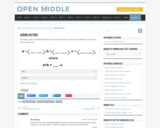
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The problem statement describes a changing algae population as reported by the Maryland Department of Natural Resources. In part (a), students are expected to build an exponential function modeling algae concentration from the description given of the relationship between concentrations in cells/ml and days of rapid growth (F-LE.2). The intent of part (b) is for students to gain an appreciation for the exponential growth exhibited despite an apparently modest growth rate of 1 cell division per day.

The purpose of the task is to help students become accustomed to evaluating exponential functions at non-integer inputs and interpreting the values.

Prior to the arrival of European colonization on the North American continent, the ecological bio-diversity was much richer than we currently know in the 21st Century. Prior to the colonization animals such as the American Bison (Bison bison), Eastern Elk (Cervus canadensis canadiensis), Eastern Cougar (Puma concolor couguar), and Wolf (Canis lupus) were commonly seen across the North American continent. However, with the colonization from the old world came old world prejudices and practices. Within two hundred and fifty years all of these species were eradicated from the Eastern United States or extinct. Over the course of the last century an effort has been made to halt the loss of the North American fauna with the creation of national parks and animal preservation habitats, and in the last half of 20th century work was being done to reintroduce that fauna back to its natural habitat. This process has been used with several different species; however, no species has been given as much attention in the Eastern United States as that of the American Elk.

This task could be used as a review problem or as an assessment problem after many different types of functions have been discussed. Since the different parameters of the functions are not given explicitly, the focus is not just on graphing specific functions but rather students have to focus on how values of parameters are reflected in a graph.

This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment.

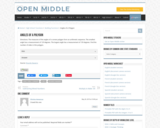
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The purpose of this task is to connect graphs with real life situations. Graphs tell a story. Specific features of a graph connect to specific features of a story. A point on a graph captures a specific instant in the story.

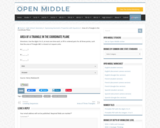
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

The purpose of this task is primarily assessment-oriented, asking students to demonstrate knowledge of how to determine the congruency of triangles.

Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.

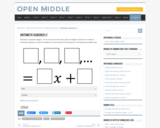
Open Middle provides math problems that have a closed beginning, a closed end, and an open middle. This means that there are multiple ways to approach and ultimately solve the problems. Open middle problems generally require a higher Depth of Knowledge than most problems that assess procedural and conceptual understanding.