Features of Rational Functions
Overview
This is a lesson plan that helps students identify the features of rational functions before they graph the rational functions. They will identify the holes, horizontal and vertical asymptotes, domain and range, and the x and y intercepts.
Summary
This lesson is to take one class period that's about 75 minutes and discuss the features of rational graphs. This lesson is to be done face-to-face, but could also be done virtually.
Background for Teachers
To teach this lesson, you will need an understanding of how to find holes, vertical asymptotes, horizontal asymptotes, zeros, and end behavior of rational functions. If you need help on the topic, the video below from YouTube can help explain the concepts, or you may look at my guided notes that are "Instruction" step of the lesson plan. You will also need my guided notes for the lesson. You may modify my notes however you would like to fit your curriculum.
https://www.youtube.com/watch?v=E1fCj5um8_c
Step 1 - Goals and Outcomes
Learning Intentions:
- Students will be able to find holes of rational functions.
- Students will be able to find vertical asymptotes of rational functions.
- Students will be able to find horizontal asymptotes of rational functions.
- Students will be able to find the x and y intercepts of rational functions.
- Students will be able to find the domain and range of rational functions.
Success Criteria:
- Students will find all holes, vertical and horizontal asymptotes, x and y intercepts, and domain and range for any rational function given.
Step 2 - Planning Instruction
Student Background Knowledge
- Prior to this lesson, students will need to have an understanding of how to simplify rational functions and how to factor. They will also need a prior understanding of what an x and y intercept is, and how to find domain and range.
Strategies for Diverse Learners
Throughout the examples, even though there isn't a graph provided, I would suggest drawing a rough sketch (not necessarily accurate in all areas). This way our visual learners, and all learners for that matter, can connect with the ideas better and see how each feature affects the look of the function when graphed.
Step 3 - Instruction
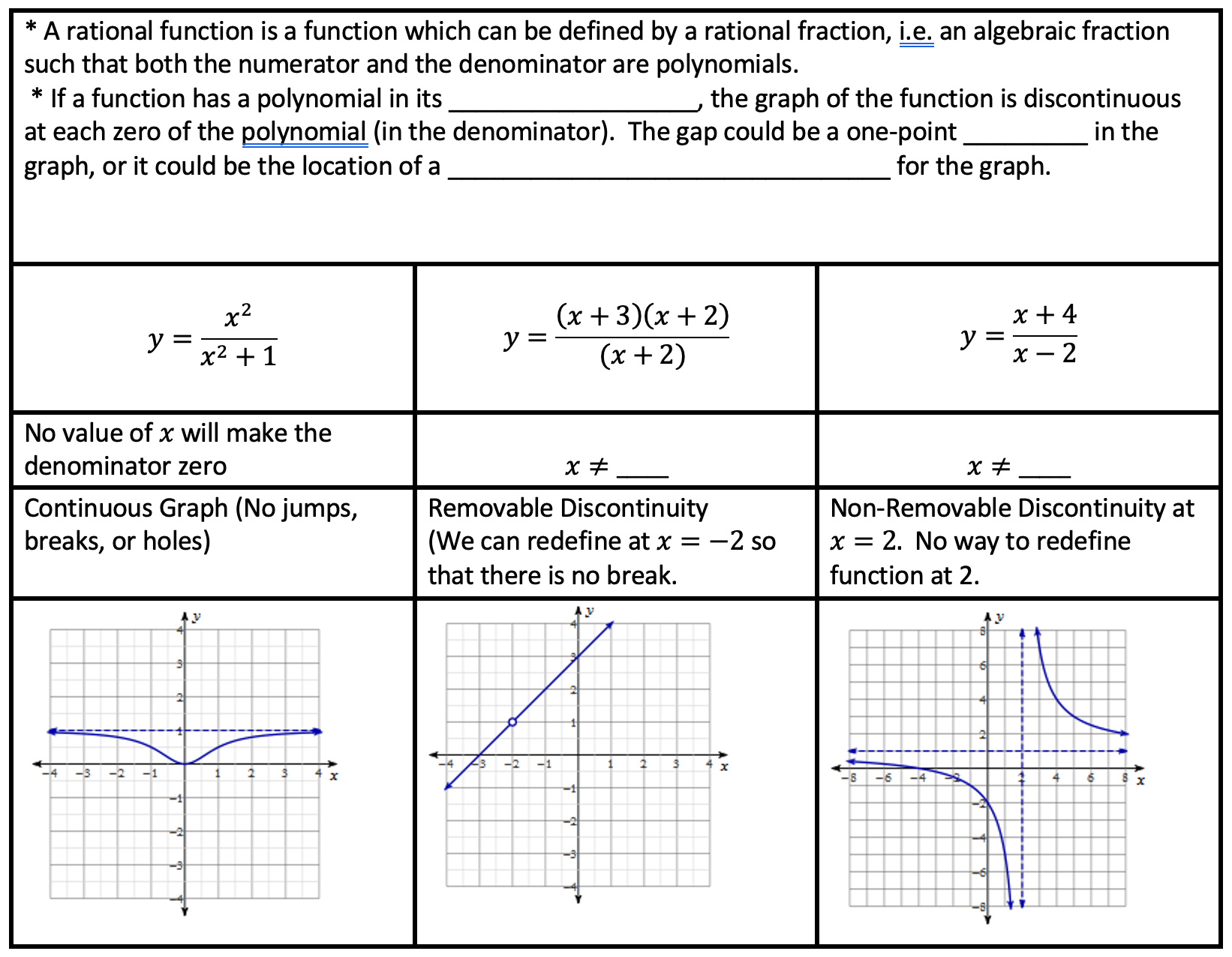
Step 1 of notes: Go through the vocab at the top and discuss the features of the three graphs. Compare and contrast them.
Step 2: Talk about the key concept at the top, fill in the missing blanks, and work through some examples shown below. For each example, I would draw a very rough sketch of the function so that students can start connecting vocab with procedure with the concept, all through the visual.
Step 3: Continue filling in blanks and going through all of the important information below. Pay close attention to the examples in the bottom right of the table: finding the asymptotes. Try to come up with an easy way to help your students understand how to remember the horizontal asymptotes rules.
Step 4: Show the students several examples. I suggest drawing a rough sketch for each example again.
Step 4 - Assessments
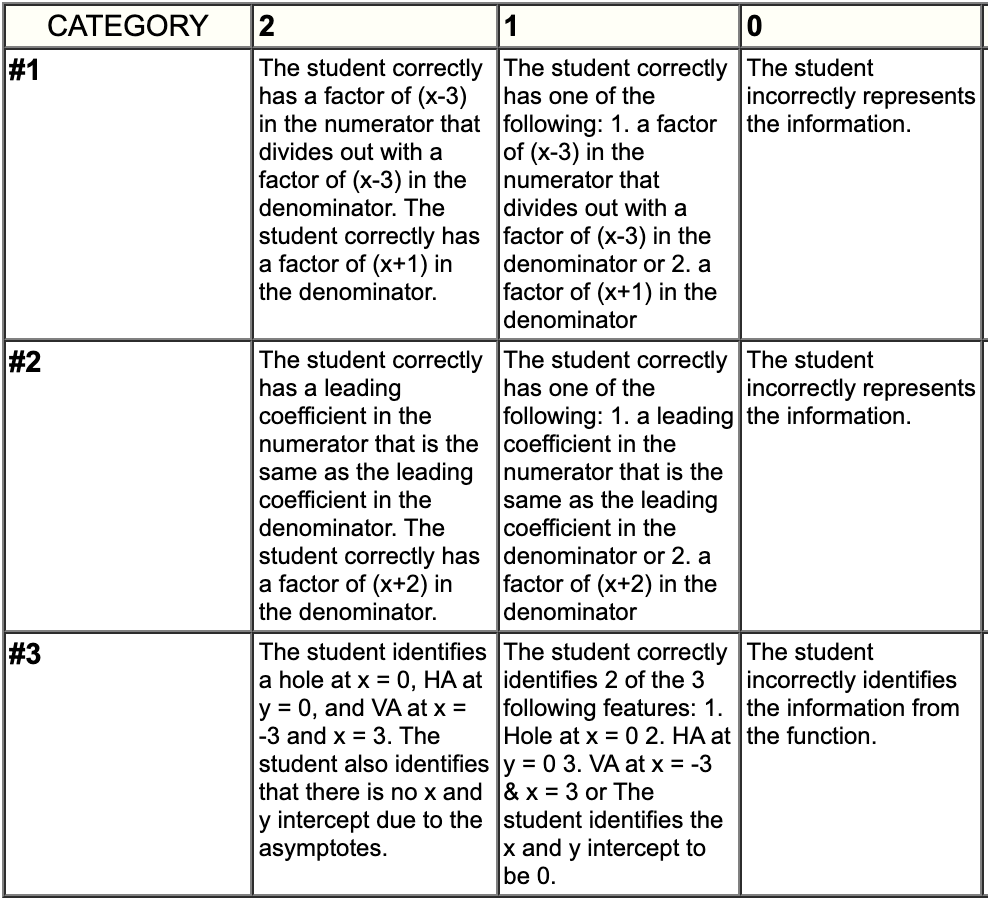
Write a rational function that meets the following conditions:
1. Hole at x = 3 and VA at x = -1 2. VA at x = -2 and HA at y = 1
Find the vertical and horizontal asymptote, domain and range, and the x-intercept and y-intercept.
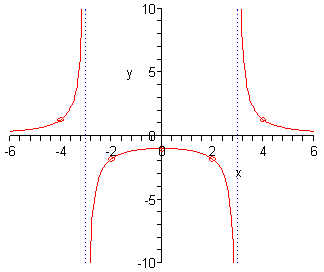
3.
Rubric: