Ipad Numbers to Calculate Standard Deviation
Overview
Content Area: Mathematics, Statistics
Lesson: Students will use Ipad Numbers to collect data and calculate Standard Deviation.
Exemplar: https://www.icloud.com/numbers/0kE5GGbPDrKdqKP5Z8WfBh6qg#Blank
Assessment: https://www.uen.org/rubric/previewRubric?id=37027
Sec Math III
Lesson Title: Standard Deviation on Ipad Numbers
Utah Core Standard: Standard S.ID.4
Use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate population percentages. Recognize that there are data sets for which such a procedure is not appropriate. Use calculators, spreadsheets, and tables to estimate areas under the normal curve.
Grade Level: Sec Math III, 11th grade
Content Area: Mathematics, Statistics
Instructional Procedures: Teacher will give a short lesson defining mean and standard deviation and its characteristics:
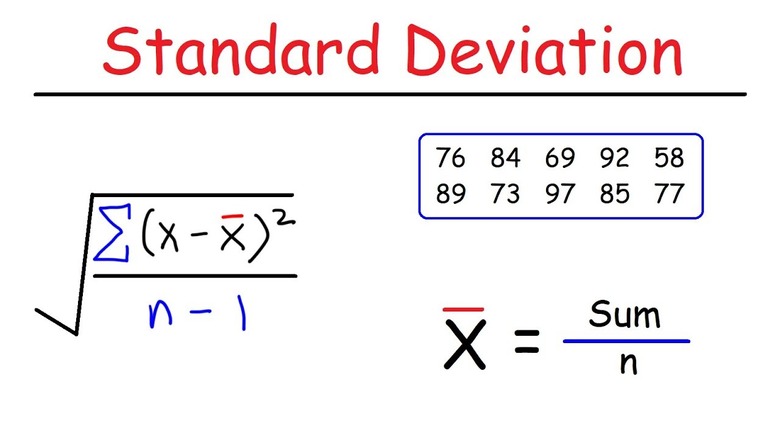
The mean of a set of data is the sum of the data values divided by the number of values. Mean is a measure of central tendency. In addition to the mean and median, which are measures of the "typical" or "middle" value, we also need a measure of how "spread out" or varied each data set is. This is a measure of variation, and one example is standard deviation. The standard deviation is a measure of variation based on measuring how far each data value deviates, or is different, from the mean.
A few important characteristics:
- Standard deviation is always positive.
- Standard deviation will be zero if all the data values are equal, and will get larger as the data spreads out.
- Standard deviation has the same units as the original data.
- Standard deviation, like the mean, can be highly influenced by outliers.
Calculating Standard Deviation:
- Find the mean.
- Find the deviation of each data from the mean. In other words, subtract the mean from the data value.
- Square each deviation.
- Add the squared deviations.
- If the data represents a whole population divide by n.
If the data is from a sample divide by n – 1
(Assume your data is a sample unless told otherwise)
6) Compute the square root of the result.
Teacher will calculate mean and standard deviation for some example data sets and lead a short discussion considering different sets of data and how the standard deviation informs the “spread” of the data:
A sample was done, collecting the data below. Calculate the standard deviation, to one decimal place.
x |
2 |
7 |
28 |
30 |
12 |
Consider these three sets of quiz scores:
Section A: 5 5 5 5 5 5 5 5 5 5
Section B: 0 0 0 0 0 10 10 10 10 10
Section C: 4 4 4 5 5 5 5 6 6 6
All three of these sets of data have a mean of 5 and median of 5, yet the sets of scores are clearly quite different. Which set has the highest standard deviation? The lowest?
Teacher will show students how to use IPad Numbers by entering data and formulas to calculate mean and standard deviation (see exemplar below).
Student Directions: Students will collect data as homework the night before this lesson. They can choose what data they would like to collect, but it must be quantitative. Examples of acceptable data:
- Height
- What age did you get your first cell phone?
- What age did you have your first kiss?
You will record your data in Ipad Numbers and use it to calculate the mean and standard deviation. You must collect at least 20 pieces of data.
Differentiation: I will have a typed set of instructions for Ipad Numbers for any students with slower processing speeds that may have trouble following at the same pace. I will also have the instructions projected on the board for EL students who may not be able to follow auditory directions as well. I will have a link to the exemplar for all students so they can access the example on their own.
Exemplar: https://www.icloud.com/numbers/0kE5GGbPDrKdqKP5Z8WfBh6qg#Blank
Assessment: https://www.uen.org/rubric/previewRubric?id=37027