In addition to the purely geometric and trigonometric aspects of the task, this problem asks students to model phenomena on the surface of the earth.

This tutorial is designed to help students understand how to solve linear equations by using the addition, subtraction, multiplication and division properties of equalities.

This task requires students to use the fact that on the graph of the linear function h(x)=ax+b, the y-coordinate increases by a when x increases by one. Specific values for a and b were left out intentionally to encourage students to use the above fact as opposed to computing the point of intersection, (p,q), and then computing respective function values to answer the question.

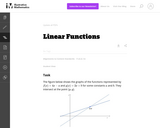
This task requires students to use the fact that on the graph of the linear function h(x)=ax+b, the y-coordinate increases by a when x increases by one. Specific values for a and b were left out intentionally to encourage students to use the above fact as opposed to computing the point of intersection, (p,q), and then computing respective function values to answer the question.

This task gives a variet of real-life contexts which could be modeled by a linear or exponential function. The key distinguishing feature between the two is whether the change by equal factors over equal intervals (exponential functions), or by a constant increase per unit interval (linear functions).

This task asks students to consider the linear and quadratic functions appearing on a coordinate plane.

The purpose of this task is to give students the opportunity to make connections between equations and the geometry of their graphs. They must read information from the graph (such as the vertical intercept of the quadratic graph or the slope of the linear one), use that information to construct and solve an equation, then interpret their solution in terms of the graph.

This task gives a variet of real-life contexts which could be modeled by a linear or exponential function. The key distinguishing feature between the two is whether the change by equal factors over equal intervals (exponential functions), or by a constant increase per unit interval (linear functions). The task could either be used as an assessment problem on this distinction, or used as an introduction to the differences between these very important classes of functions.

This is an instructional task that gives students a chance to reason about lines of symmetry and discover that a circle has an an infinite number of lines of symmetry. Even though the concept of an infinite number of lines is fairly abstract, fourth graders can understand infinity in an informal way.

This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. It is both interesting and important that these types of quadrilaterals can be distinguished by their lines of symmetry.

This task is intended for instruction, providing the students with a chance to experiment with physical models of triangles, gaining spatial intuition by executing reflections.

This is a challenging fraction comparison problem. The fractions for this task have been carefully chosen to encourage and reward different methods of comparison.

In this number line task students must treat the interval from 0 to 1 as a whole, partition the whole into the appropriate number of equal sized parts, and then locate the fraction(s).

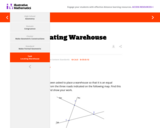
This task can be implemented in a variety of ways. For a class with previous exposure to the incenter or angle bisectors, part (a) could be a quick exercise in geometric constructions,. Alternatively, this could be part of a full introduction to angle bisectors, culminating in a full proof that the three angle bisectors are concurrent, an essentially complete proof of which is found in the solution below.

This task can be implemented in a variety of ways. For a class with previous exposure to the incenter or angle bisectors, part (a) could be a quick exercise in geometric constructions,. Alternatively, this could be part of a full introduction to angle bisectors, culminating in a full proof that the three angle bisectors are concurrent, an essentially complete proof of which is found in the solution below.

In this instructional task students are given two inequalities, one as a formula and one in words, and a set of possible solutions. They have to decide which of the given numbers actually solve the inequalities.

This task is for instructional purposes only and students should already be familiar with some specific examples of logistic growth functions such as that given in ''Logistic growth model, concrete case.''

The goal of this task is to have students appreciate how the different constants (P0, K, and r) influence the shape of the graph.

This problem introduces a logistic growth model in the concrete setting of estimating the population of the U.S.