This task provides a context for performing division of a whole number by a unit fraction. This problem is a "How many groups?'' example of division.

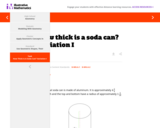
This task's main goal is to provide a familiar context and a straightforward question which require a variety of tools to solve: modeling a situation with geometry, paying close attention to units, and converting units.

This is a variation of ''How thick is a soda can? Variation I'' which allows students to work independently and think about how they can determine how thick a soda can is.

Students play a game in pairs to read and recognize numbers using a 100 chart.

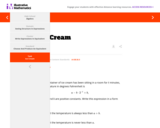
This task illustrates the process of rearranging the terms of an expression to reveal different aspects about the quantity it represents, precisely the language being used in standard A-SSE.B.3. Students are provided with an expression giving the temperature of a container at a time t, and have to use simple inequalities (e.g., that 2t>0 for all t) to reduce the complexity of an expression to a form where bounds on the temperature of a container of ice cream are made apparent.

This task illustrates the process of rearranging the terms of an expression to reveal different aspects about the quantity it represents, precisely the language being used in standard A-SSE.B.3.

This rich task is an excellent example of geometric concepts in a modeling situation and is accessible to all students. In this task, students will provide a sketch of a paper ice cream cone wrapper, use the sketch to develop a formula for the surface area of the wrapper, and estimate the maximum number of wrappers that could be cut from a rectangular piece of paper.

This rich task is an excellent example of geometric concepts in a modeling situation and is accessible to all students. In this task, students will provide a sketch of a paper ice cream cone wrapper, use the sketch to develop a formula for the surface area of the wrapper, and estimate the maximum number of wrappers that could be cut from a rectangular piece of paper.

The purpose of this Illustrative Mathematics task is to engage students, probably working in groups, in a substantial and open-ended modeling problem. Students will have to brainstorm or research several relevant quantities, and incorporate these values into their solutions.

The purpose of this task is to engage students, probably working in groups, in a substantial and open-ended modeling problem. Students will have to brainstorm or research several relevant quantities, and incorporate these values into their solutions.

The goal of this task is to interpret the graph of a rational function and use the graph to approximate when the function takes a given value.

This task includes an experimental GeoGebra worksheet, with the intent that instructors might use it to more interactively demonstrate the relevant content material.

In this task students use algebraic methods to determine whether each of the functions is odd, even, or neither.

This task emphasizes the expectation that students know linear functions grow by constant differences over equal intervals and exponential functions grow by constant factors over equal intervals.

This task emphasizes the expectation that students know linear functions grow by constant differences over equal intervals and exponential functions grow by constant factors over equal intervals.

The goal of this task is to get students to focus on the shape of the graph of the equation y=ex and how this changes depending on the sign of the exponent and on whether the exponential is in the numerator or denominator. It is also intended to develop familiarity, in the case of f and k, with the functions which are used in logistic growth models, further examined in ``Logistic Growth Model, Explicit Case'' and ``Logistic Growth Model, Abstract Verson.''

The goal of this task is to work on finding multiples of some whole numbers.

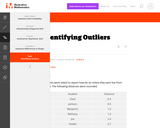
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.